ドッカノっていう名前の放牧地にいるってことですはい
今回は
↑(クヌースの矢印表記)について書いていこうと思います
こんなただの↑ですがこれ数学で使われます。
(中学生や高校生お馬さんでいうと2歳馬3歳馬くらいだと)
↑で数学って言ったら“ベクトル”をイメージするかも知れませんがそれではなくて、足し算や掛け算または
べき乗(=10の2乗や3の3乗)と同じように
数を大きくする働きがあります。
ハイパー演算子
ハイパー演算子というものがあります
足し算がハイパー演算子1掛け算がハイパー演算子2
べき乗がハイパー演算子3 とかいう言い方をしています
でハイパー演算子4やさらに上
を表すのに”↑”を使います
この”↑”を使った表記はクヌースの矢印表記と言われていて、クヌースは人間の名前です
1976年にロナルド=クヌースという数学者が日常的には使わないような想像を絶する巨大な数を表すために作ったものです。
(Wikipediaより)


クヌースの矢印表記はタワー表記とも呼ばれていますがここではクヌースの矢印表記に統一します。
(少なくても馬の僕には意味不明です)
なので比べてみるとお分かり頂けるかと思います。
足し算と掛け算
まず3で
3+3+3=9 (足し算:ハイパー演算子1)
3×3=9 (掛け算:ハイパー演算子2)
5+5+5+5=20 (ハイパー演算子1)
5×4=20(ハイパー演算子2)
足し算(ハイパー演算子1)だったら、9にするために3を3つ持ってくる必要がありました
が掛け算(ハイパー演算子2)なら2つで済みました。
また“掛け算の後ろの数字”は”足し算で行う場合
もう前の数字”をいくつ持って来たらその数に達するのか表していないでしょうか?
掛け算とべき乗
続いて掛け算とべき乗を比べます
3×3×3=27(掛け算:ハイパー演算子2)
3^3=27(べき乗:ハイパー演算子3)
4×4×4×4×4=1024(ハイパー演算子2)
4^5=1024(ハイパー演算子3)
※ ^は”キャレット“と読み
べき乗(指数)を表すのに使い
数字の上に小さく数字を書いた場合と同じです。
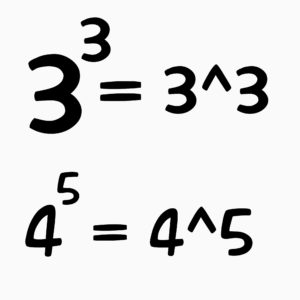
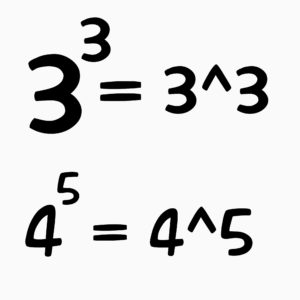
掛け算(ハイパー演算子2 )だったら3を3つ持ってこないと27にはなりませんが
ベき乗(ハイパー演算子3)なら2つで済みます。
足し算から掛け算にランクアップしたときと同じく
べき乗の後ろの数字は、掛け算で表した場合 前の数字を何回掛けたらその数字に達するか表しています。
そしてべき乗レベルになるとかなり大きな数を比較的コンパクト表すことができます。
上の例で行くと掛け算だったら4を5つ持ってきてやっと1024にまで大きくなってしまいますが
べき乗だと”4と5の間に^を入れただけ“で
1024です。
なので普通に暮らしていたら、べき乗まで知ってたらやっていけます。
しかしべき乗はハイパー演算子3
なのでその上にクヌースの矢印表記↑
(ハイパー演算子4:テトレーション)
なんていうさらにアホみたいに急激に
大きくすることができます。
いったいどれくらい大きくなっていくのでしょう?
べき乗からテトレーションに


ここからは↑(クヌースの矢印表記)を
使って行きましょう。
3^3=27
これをクヌースの矢印表記で書くと
3↑3になり
4^5=1024なら 4↑5になります。
3^3^3=これは3の3の3乗乗と読み
3^27と同じ大きさになります
もはや頭で計算することができませんね
しかしまだハイパー演算子3べき乗です
ちなみに計算すると
=7625597484987
7兆6255億9748万4987になります。
こんなアホみたいに大きな数をクヌースの
矢印表記だったら
3↑↑3と
書けてしまいます。
さらに
3↑↑4=3↑3↑3↑3=3^7625597484987
3↑↑5=3↑3↑3↑3↑3=3^3^7625597484987
4↑↑3=4↑4↑4=4^64
4↑↑4=4↑4↑4↑4=4^4^64
もはや計算すらできないほどの
数になってしまいました
クヌースの矢印表記は↑1本なら
ハイパー演算子3=べき乗
2本書いたら
“ハイパー演算子4=(テトレーション:超べき乗)になります
テトレーションからさらに上へ
ハイパー演算子4(テトレーション)
があるなら5もあるだろう?そうですあります。
ハイパー演算子5もクヌースの矢印表記で
3↑↑↑3
と書くことができます。
どんな数かというと3↑↑↑3=3↑↑(3↑↑3)
つまり3↑↑7625597484987 となります
3の3の3の..(約7兆6千億回)の乗乗乗乗(約7兆6千億回)乗乗という想像を絶するものです。
そして↑を4本にすれば
ハイパー演算子6になります
3↑↑↑↑3
こんな感じになりこの左右の数が3になっていて中に矢印表記が4本あったらG1ともいいます。
このG1の Gの意味は次回の数遊びで解説します。
感想(まとめ)
足し算は ハイパー演算子1 掛け算はハイパー演算子2べき乗はハイパー演算子3
だからその上に
ハイパー演算子4 ハイパー演算子5 ハイパー演算子6とどこまでもある
クヌースの矢印表記を使うと想像を絶するほどの数発狂するほどの大きさの数が簡単に作れる
3↑↑↑↑3=G1?なんだそれ
そろそろ頭がパンクしたかと思うのでここらへんで終わりです


最後まで読んでいただきありがとうございます